SealQuickSearcher

（４）密封理論

（ａ）基礎理論
グランドパッキンの密封理論にはD.F.DennyやD.E.Turnbull1)の研究がある。
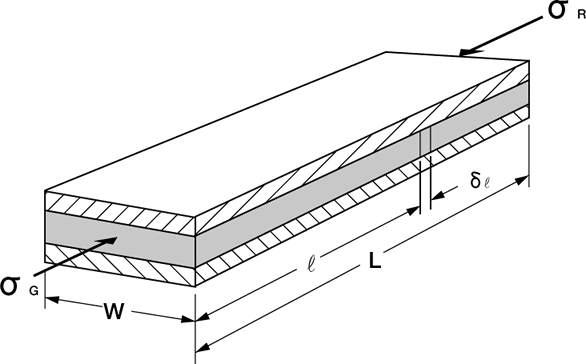
D.F.Dennyは図1.3.1のような２つの金属壁に挟まれたパッキンに圧縮応力σ_Gを与えたときの内部応力の平衡状態を図1.3.2のように表した。

＜技・製＞　図1．3．1　金属壁に挟まれたパッキン

＜技・製＞　図1．3．2　パッキン内部応力の平衡状態

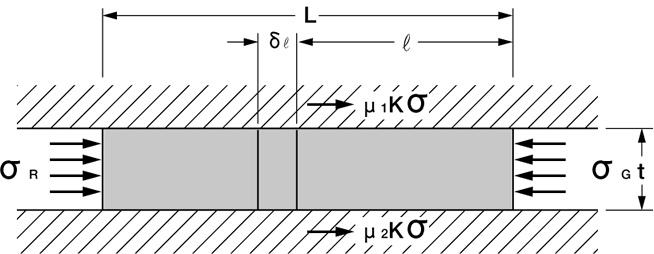
パッキン内部では、図1．3．2のごとく応力のバランスが生じ、パッキンの任意の点で σ＋δσとそれに対する反力σおよびμKσとが平衡状態となる。
またそのとき壁面にはK_σという力が生じる。ここでKは、そのパッキンがもつ固有の係数であって一般には 0.6～1.0の間にある。

これを式で示すと

（２）式を積分し、ℓ＝0の時P＝P_Gとなるのでこれを代入することにより（３）式が得られる。

この式は、締付応力σ_Gを与えたときのスタフィングボックス内部の応力分布を示す式である。
次にこの式を応用し、実際にパッキンをスタフィングボックス内に詰め込んだ場合の内部応力の算出式を求めてみる。

＜技・製＞　図1．3．3　スタフィングボックス内のパッキンの応力分布

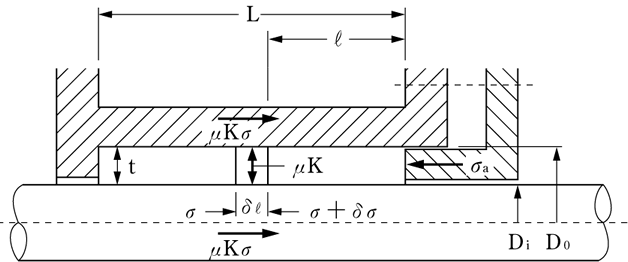
図1．3．3において、パッキンの形状を断面正方形と仮定し、μ₁＝μ₂＝μとすれば、

であるから、これを（３）式に代入すると

ここでrを各リングの下面を基準にとり、１リングあたりの高さをh、圧縮前に対する圧縮後のパッキン高さの比率をCとすると

今、Cを0.8とおくと

（４）式および（７）式から

この（８）式に、NおよびμK値を入れることでスタフィングボックス内の任意の点の圧縮応力を求めることができる。
なお、μ値およびK値はパッキンの軸しゅう動係数μKという形で実測される。
表1．3．7 に代表的なパッキンのμK値を示す。

＜技・製＞　表1．3．7　代表的なパッキンのμK値

項目とパッキンの種類	μK値（無次元）		代表的なバルカーNo.
項目とパッキンの種類	起動時	しゅう動時	代表的なバルカーNo.
潤滑処理バルフロン含浸炭素繊維パッキン	0.02～0.03	0.01～0.02	6232、6262、6399L
バルフロン含浸特殊繊維パッキン	0.03～0.04	0.02～0.03	8137
バルフロン繊維パッキン	0.03～0.04	0.02～0.03	7233　7232
膨張黒鉛パッキン	0.07～0.09	0.04～0.06	VF-10、VF-20
低トルク処理膨張黒鉛パッキン	0.03～0.05	0.03～0.04	VFC-25、VF-20LF
PTFE破覆膨張黒鉛パッキン	0.02～0.03	0.02～0.03	VFT-22

また、パッキン装着締め付け後にσ_Gを維持しながら軸作動をさせた場合の締付面圧の変化を求めると、次のようになる。図1.3.3において軸を左へ移動させたとき、それによって伝達されるパッキンの締付力が μK_σより30％多く発生したとすると、

標準サイズのパッキンをD_o＝32、D_i＝20として
（D_o－0.3D_i）/（D_o＋D_i）＝0.5であるから

これをまとめるとパッキン締め付け後軸作動をしない場合

パッキン締め付け後軸作動をした場合

（イ）漏れ

漏れ量Qは大略

ここでℓ′：スタフィングボックス奥部から取ったパッキン長さ

：軸面に働く流体圧力の勾配

Dennyらの研究によれば、流体圧力P_f が締付圧力P_Gに対し影響を与えない程度であれば、シール性はP_Gのみによって支配され、漏れ量QはP_G²に反比例しP_fに比例する。

またP_f が非常に高い場合は、密封作用は自動的となりパッキン押えに近い10％ぐらいの部分でのみ密封し、他の部分は密封にもトルクにも関与しない。したがって装着リング数は、密封作用には無関係である。

（ロ）軸抵抗

（16）式に（３）式を代入することで

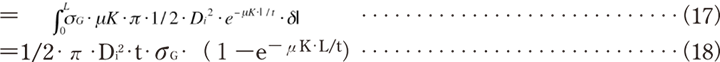
したがって、概略的には以下の通りとなる。

（ｂ）ポンプ・機器用途での漏洩量の推定
グランドパッキンの動的シールとしての使用に際して、漏洩量の推定値を算出する。
なお、推定対象は非圧縮性の粘性流体で層流状態での漏れを前提とする。

（イ）回転用途の場合
回転する円筒と静止した軸の間、あるいは静止円筒と回転軸との間のきわめて狭いすき間を流れる漏れ流れについては、すき間をｓとした場合、次の関係式が求められている。

D：軸径 ΔP：差圧（P1－P2） P1：流体圧力
P₂：大気圧（通常） η：流体の粘度 r：シール長さ（締め付け後のパッキン装着長)

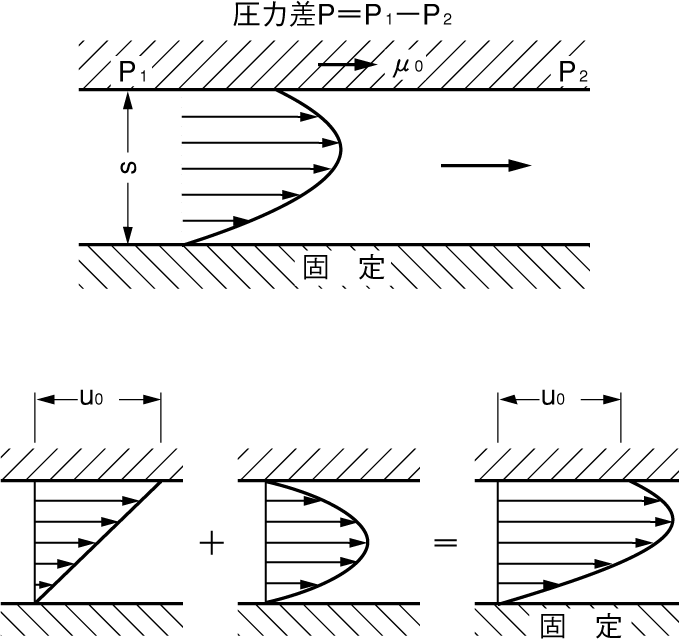
（ロ）往復動用途の場合
漏れの方向に直角方向の壁の運動は、層流状態では漏れには影響しないが、漏れの方向の壁の運動は漏れに影響する。この場合は運動壁が引っ張る作用と、圧力差による固定壁間の漏れ流れの和となり、単位幅あたりの漏れ量Qは

で表される。

すき間sを直径の円筒状のすき間と考えた場合には、（23）式のQの値に円周長さπDを乗じて

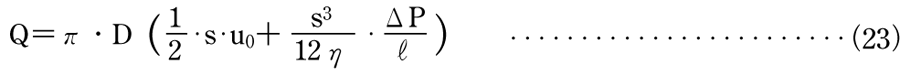
によって漏れ量を求めることができる。
ただし、壁の運動方向と圧力の働く方向が反対の場合には