SealQuickSearcher(中国語)

（４）密封理论

（ａ）基础理论
对于填料密封的密封理论，有 D.F.Denny 及 D.E.Turnbull 1）的研究。
D.F.Denny 是如图1.3.1 所示，在夹在 2 块金属板之间的填料上施加以压缩应力 G ，此时的内部应力平衡状态如图 1.3.2 所示。

＜技・製＞　图 1. 3. 1　被夹在金属板之间的填料

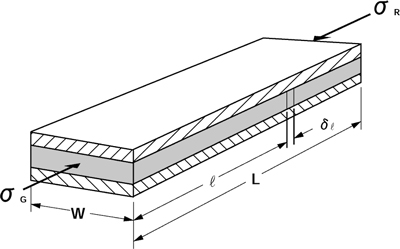
＜技・製＞　图 1. 3. 2　填料内部应力的平衡状态

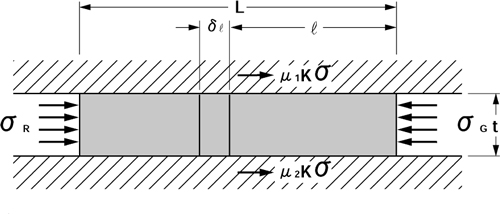
在填料的内部，如图 1.3.2 所示产生应力的平衡，在填料的任意一点上，σ+δσ 和与之相对的反作用力 σ 及 μKσ 处于平衡状态。
并且此时，对板面产生 Kσ 的力。在这里，K 是该填料固有的系数，一般在 0.6～1.0 之间。

以公式表示即

积分（2）式，得出＝0 时的 P＝PG，将其代入得到（3）式。

该式是表示当施加以紧固应力 σ_G 时，填料箱内部应力分布的表达式。
然后，应用该式，求出将填料实际嵌入填料箱内时的内部应力计算公式。

＜技・製＞　图 1. 3. 3　填料箱内的填料的应力分布

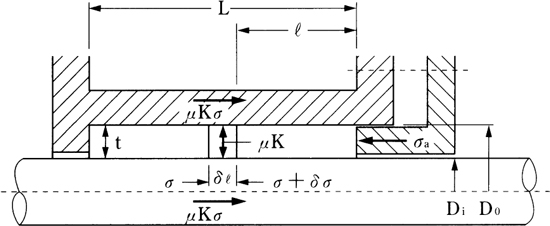
图 1.3.3 中，假定填料的形状为正方形截面，如果令μ₁＝μ₂＝μ由于

将其代入（3）式中，则

此时，以各圈的下面为基准取，以 1 个圈的高度为 h，以压缩后高度相对于压缩前高度的比率为 C，则

现在，如果 C 取 0.8，则

由（4）式及（7）式得

通过向（8）式中代入 N 及 μ K 的值，能够求出填料箱内任意一点的压缩应力。
另外，μ 值与 K 值以填料的轴滑动系数 μ K 的形式通过实测获取。
表 1. 3. 7 中，给出了具代表性的填料的 μ K 值。

＜技・製＞　表1．3．7　代表性的填料的 μ K 值

项目和填料的种类	μK値（无次元）		代表性的华尔卡No.
项目和填料的种类	启动时	滑动	代表性的华尔卡No.
润滑处理华尔氟龙浸渍碳纤维填料	0.02～0.03	0.01～0.02	6232、6262、6399L
华尔氟龙浸渍特殊纤维填料	0.03～0.04	0.02～0.03	8137
华尔氟龙纤维填料	0.03～0.04	0.02～0.03	7233　7232
膨胀石墨填料	0.07～0.09	0.04～0.06	VF-10、VF-20
低扭矩处理膨胀石墨填料	0.03～0.05	0.03～0.04	VFC-25、VF-20LF
PTFE包覆膨胀石墨填料	0.02～0.03	0.02～0.03	VFT-22

此外，安装紧固填料后，在维持 σ_G 的同时令其进行轴动作时，求出紧固面压的变化如下。
图 1.3.3 中，如果设定当轴向左侧移动时，因之传递的填料的紧固力比 μK_σ 多30%，则

设标准尺寸的填料为D_o＝32、D_i＝20则由于
（D_o－0.3D_i）/（D_o＋D_i）＝0.5所以

综合以上可得
填料紧固后，当不进行轴动作时

填料紧固后，当进行轴动作时

（甲）泄　漏

泄漏量 Q 以

此处 ℓ′：在填料箱内部获取的填料长度

：作用于轴面的流体压力的倾角

根据 Denny 等的研究，如果流体压力 Pf 不足以对紧固压力 P_G 产生影响，则密封性仅受 P_G 的影响，泄漏量 Q 与 P_G^{2>/sup> 成反比，与 Pf 成正比。}

而当P_f 非常高时，密封作用仅由填料紧固部位的 10% 左右的部位完成，其它的部分对于密封及扭矩不产生影响。因此，安装环数与密封作用没有关系。

（乙）轴阻力

将（3）式代入（16）式中可得

因此，基本上如下。

（ｂ）推算泵、机器中的泄漏量
将填料密封用于动密封时，算出的泄漏量的估算值。
并且，估算对象为非压缩性的粘性流体，且以层流状态下的泄漏为前提。

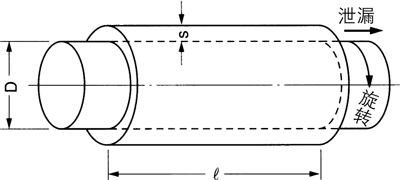
（甲）旋转用途
对于从旋转的圆筒与静止的轴之间，或是从静止圆筒与旋转轴之间的极狭窄的游隙中流出的泄漏量，设游隙为 s，则可求出以下的关系式。

D：轴径 ΔP：压差（P1－P2） P1：流体压力
P₂：大气压（通常） η：流体的粘度 r：密封长度（紧固后的密封圈安装长度）

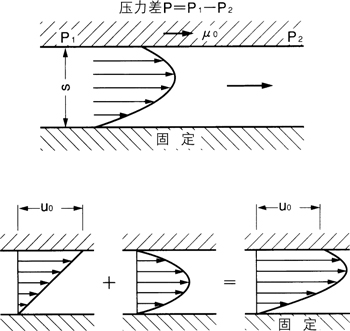
（乙）往复运动用途
与泄漏方向成直角方向的壁运动，在层流状态下，不会影响到泄漏，但是泄漏方向的壁运动，将会对泄漏产生影响。此时，泄漏量为运动壁拉伸作用与因压力差而导致的固定壁间的泄漏流量的和，单位宽度上的泄漏量 Q，以

来表示。

当把游隙 s 认为是直径的圆筒状游隙时，（23）式的 Q 的值与圆周长度 πD 相乘

可根据上式求出泄漏量。
但是，当压力的作用方向与壁的运动方向相反时，则